算法的优劣主要从时间和空间两方面进行分析：

时间：是指执行当前算法所消耗的时间，我们通常用「时间复杂度」来描述。

空间：是指执行当前算法需要占用多少内存空间，我们通常用「空间复杂度」来描述。

时间复杂度:

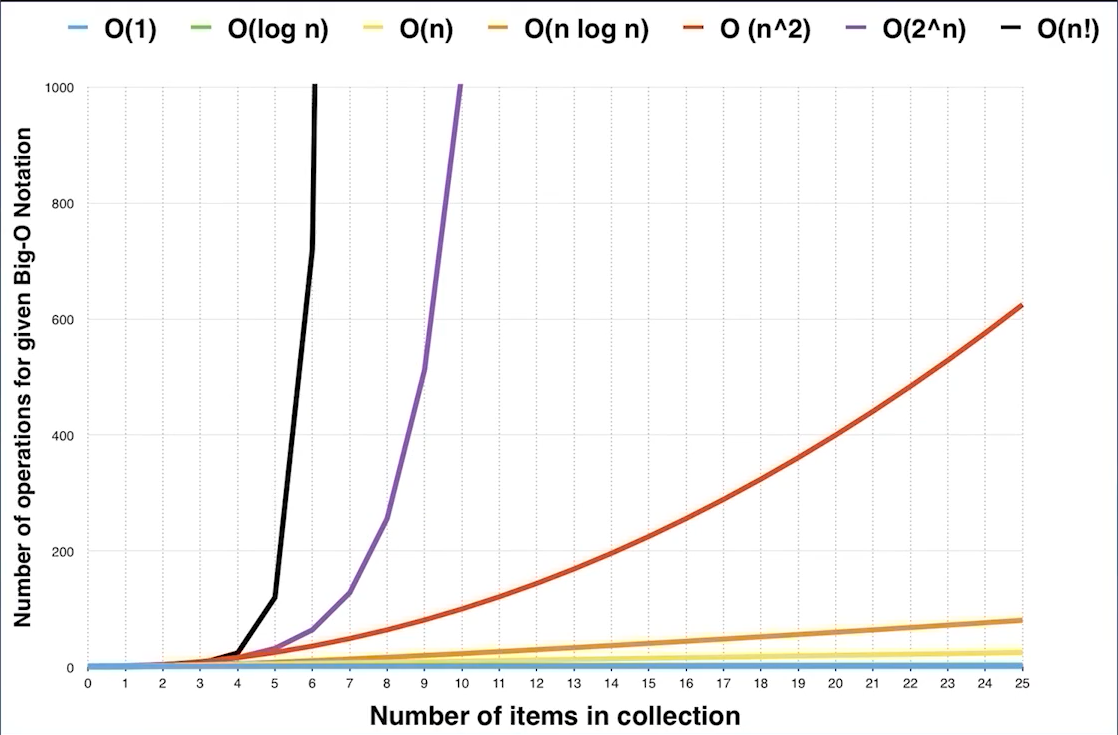
常见的七种时间复杂度

O（1）：Constant Complexity 常数复杂度

O（log n）：Logarithmic Complexity 对数复杂度

O（n）：Linear Complexity 线性时间复杂度

O（n^2）：N square Complexity 平方

O（n^3）：N cubic Complexity 立方

O（2^n）：Exponential Growth 指数

O（n!）：Factorial 阶乘

注:用到多种时,只看最高复杂度的运算

七种时间复杂度曲线:

image-20200823233037517

举例

计算：1+2+3+4+…+n

方法一：从1到n的循环累加 

1
2
3
4
int sum=0;
for(int i=0;i<n;i++){
	sum+=i;
}

此方法循环了 n 次，时间复杂度为 O(n)。

方法二：公式法 sum = n (n+1)/2

1
int sum = n(n+1)/2

此方法只运行一步，时间复杂度为 O(1)。

斐波那契额数列:

递归法：

1
2
3
4
int fib(int n){
	if(n<2) return n;
	return fib(n-1) + fib(n-2);
}

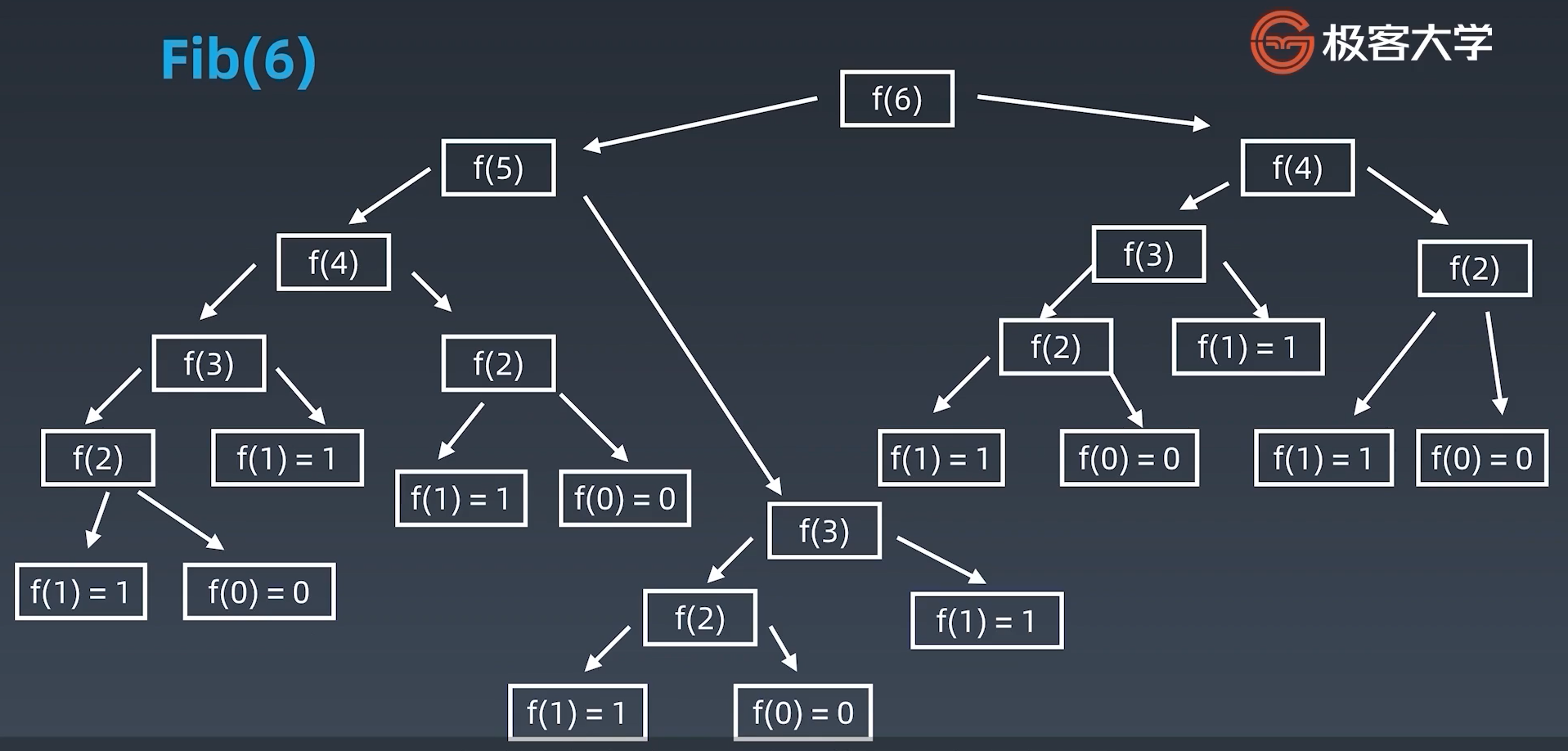
递归树：

image-20200823233641687

斐波那契数列递归解法存在大量的冗余，在这里先不做优化，只看时间复杂度为O(2^n)

主定理

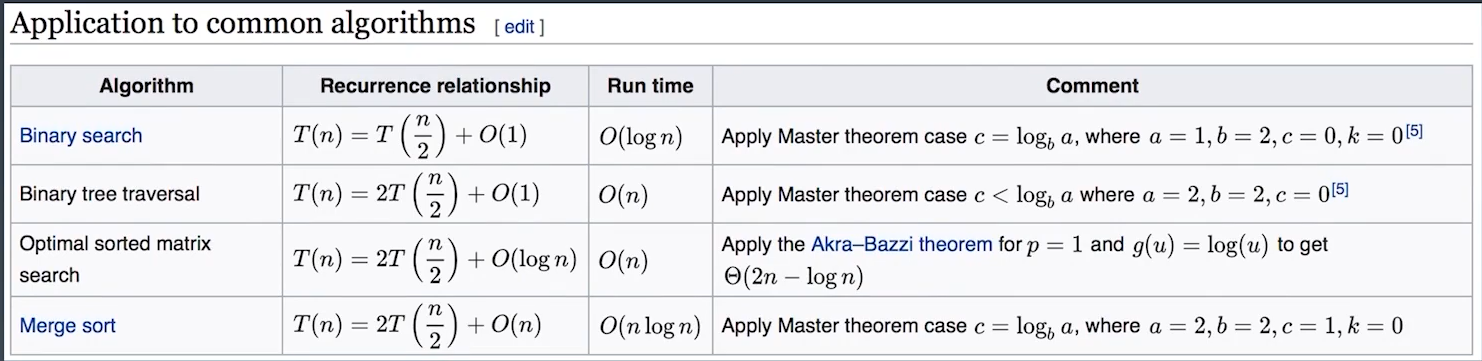
image-20200823235634487

二分查找: O(log n)

二叉树遍历: O(n)

二维矩阵（有序）二分查找: O(n)

归并: O(nlog n)

主定理证明比较复杂，只记住这四种即可。

思考:

二叉树遍历-前序、中序、后序：时间复杂度是多少？
图的遍历：时间复杂度是多少？ O(n)
搜索算法：DFS、BFS时间复杂度是多少？ O(n)
二分查找：时间复杂度是多少？ O(log n)

空间复杂度

空间复杂度取决于以下因素:

  1. 数组的长度

    一维数组 O(n)

    二维数组 O(n^2)

  2. 递归的深度

    注: 递归里面开数组,空间复杂度为两者中的最大值

上述斐波那契额数列的递归解法的空间复杂度为递归的深度，即O(n);