极客-第二次课堂笔记
二叉树的基础内容
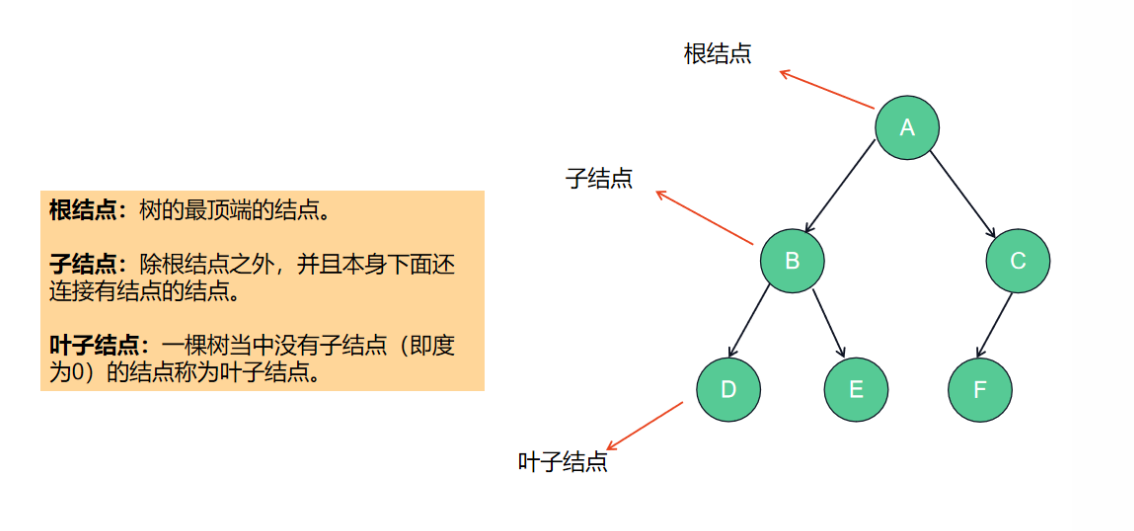
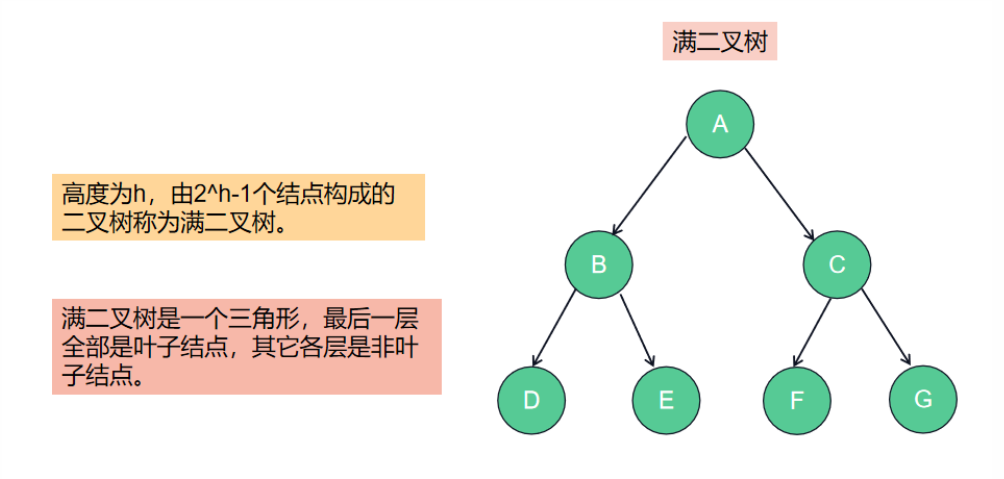
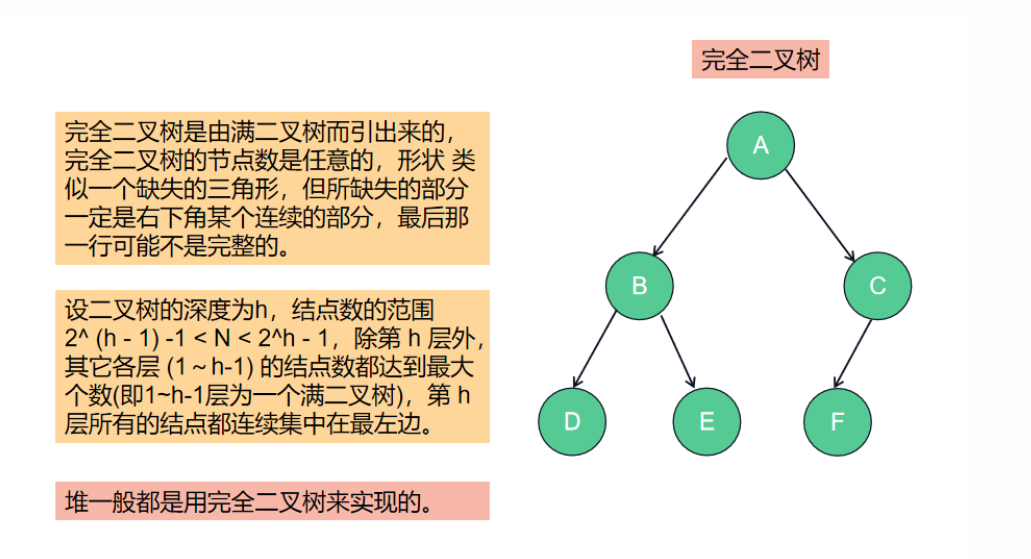
《验证二叉搜索树》

通过二叉搜索的性质,我们能想到只需遍历整棵树,并判断 node.left.val < node.val < node.right.val 对于每个结点是否成立。
需要注意的是不仅左子结点(右子结点)需要小于(大于)该结点,而且整个左子树(右子树)的所有的元素都应该小于(大于)该结点。所以我们在遍历的同时需要同结点的上界和下界比较。
方法一:递归 + 前序遍历
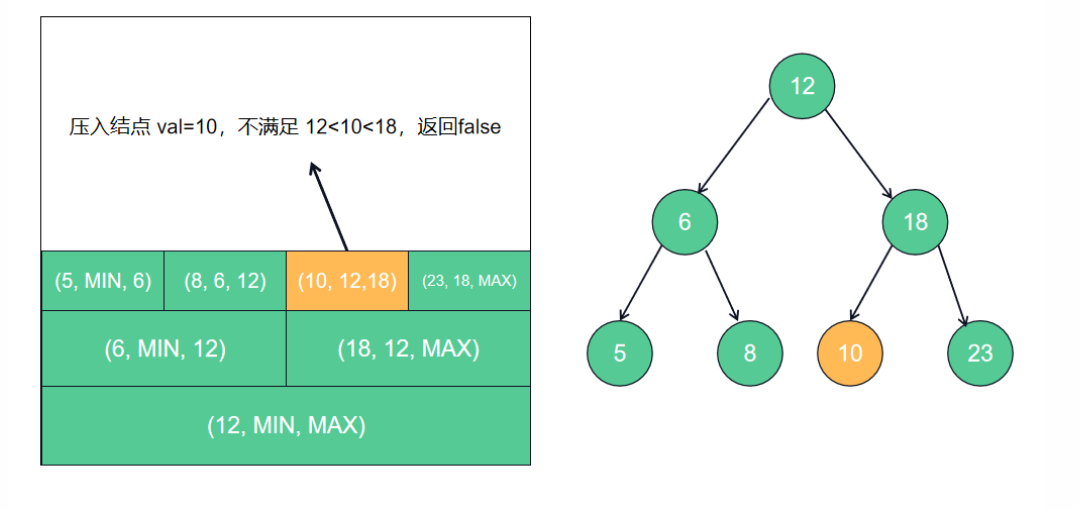
上述的思路可以通过递归的方法实现,将当前结点的值与上下界进行比较,然后在对左右子树进行递归。过程如图所示:
如果当前结点的值应检验无效时,返回false。
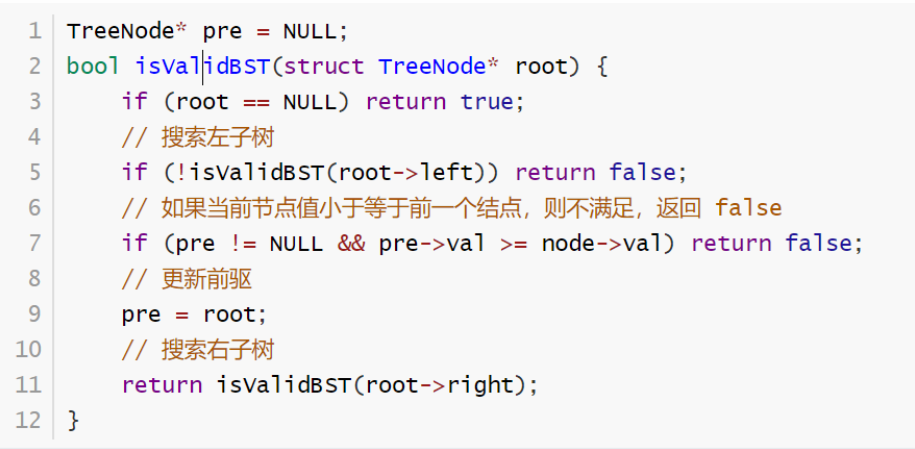
源码如下:
方法二:递归 + 中序遍历
我们也可以采用中序遍历的方式,因为中序遍历后的二叉搜索树是有序的,所以只需判断一次当前结点的值即可。
方法三:栈 + 中序遍历
基于栈实现中序遍历。
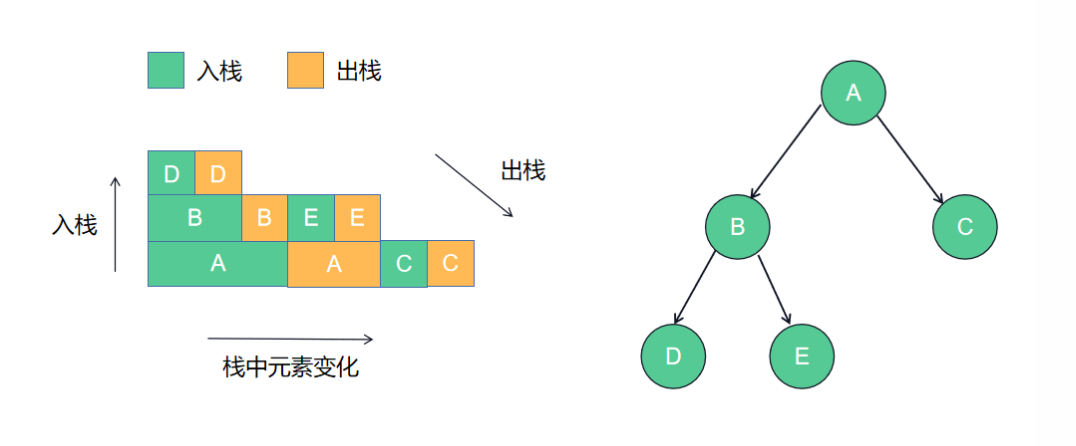
接下来讲解一下如何使用栈实现前中后序遍历,以栈实现中序遍历为例,过程如下图:
栈实现中序遍历模板及关键点:
栈实现先序遍历:
栈实现后序遍历:
综上, 我们分析了递归和栈实现《验证二叉搜索树》的思路。并且学习了二叉树的先中后序遍历。
层序遍历
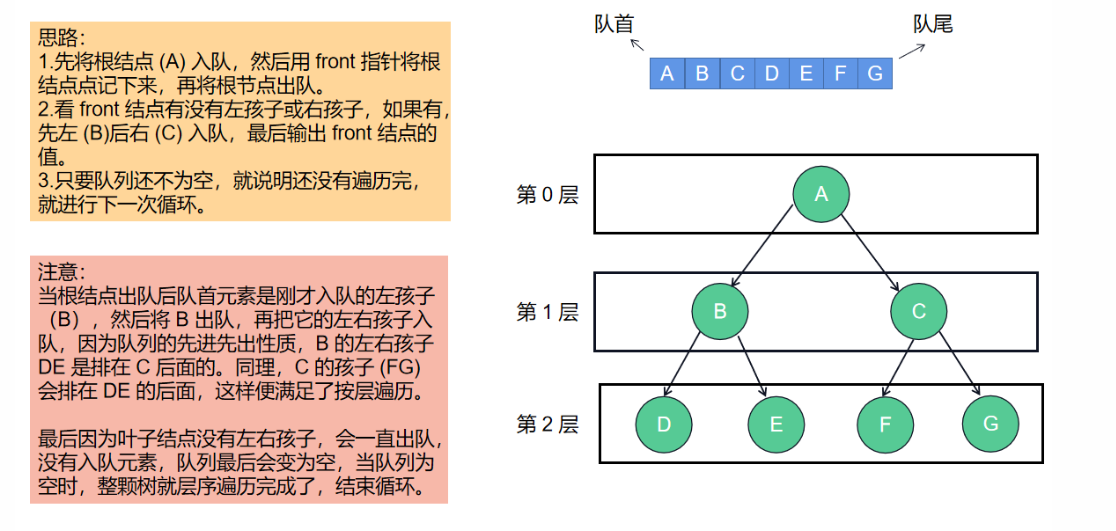
现在再给大家介绍一种遍历方式——层序遍历,层序比遍历非常好理解,就是将二叉树的每一层分遍历,直到最后所有的结点全部遍历完成,这里我们需要的辅助数据结构是队列,因为需要用到队列先进先出的特性。
模板代码如下:
大家可以做一下LeeCode102题《二叉树的层序遍历》,进一步理解层序遍历的思想和代码。
《二叉树的最大深度》
接下来我们看下《二叉树的最大深度》, 这道题目根据我们上面总结的内容,不难写出来。
注意使用递归和栈实现二叉树的前中后序遍历的是非常重要,很多题目都会涉及到二叉树的遍历,所以大家一定要多加练习,保证能够熟练的写出来。大家可以尝试去完成 LeetCode 中二叉树的前中后序遍历的题目,进行巩固练习。
综上, 我们分析了递归和栈实现 《验证二叉树》《二叉树的最大深度》的思路和源码 并给出拓展,